As usual, I have too many projects going at once, and this MU blog suffers. I have been slogging through Pearl's Probablistic Reasoning in Intelligent Systems; bookmark last left at the end of the section "2.1.4 Recursive Bayesian Updating." Also continuing Kuffler et al's From Neuron to Brain, where I just finished reading about GABA, a neurotransmitter for inhibitory synapses. I doubt the specific biochemistry of synapses will be much help in MU, but sometimes it gets me thinking, and sometimes I do some biotechnology analysis and investing, so the database accumulation can't hurt.
People are already applying some of Numenta's HTM technology. In case you missed it, Vitamin D, Inc. has a beta you can try, Vitamin D Video. It apparently can pick out objects from a webcam video stream. On the one hand that is very impressive, on the other hand it is a long, long way from machine understanding. Typical of my hands-off style, for years I contemplated how I could get my computer to watch my aquarium, and inentify and track the fish in it. I never came up with a good enough plan to try to implement.
The section in Kuffler I just started reading made me think about animal rights and machine understanding issues because one of the animal models for the neurotransmitter discussed, an LHRH analogue (or apparently now GnRH analogue), was based in part on studying frogs. I have tended to have the view that understanding and consciousness go together, and that only a few species of animals have much in the way of understanding. I was thinking about whether experimenting with a frog's nerves is a form of torture. In the past I would have said no, but I am not so certain. Frog neural systems are very, very complicated, if only a tiny fraction compared by size to human neural systems. Since I can't say with certainty how human understanding or consciousness work, I can't be certain if a frog understands anything, or if a lack of understanding implies lack of conciousness. Which may just put the animal rights debate on a different level: should animals have rights just because (if) they are conscious?
One great thing about working with computer models for "artificial intelligence" is that no one is being tortured, except maybe the computer programmers.
Friday, December 11, 2009
Saturday, November 14, 2009
Review of Towards a Mathematical Theory of Cortical Micro-circuits
This is a report on my first reading of "Towards a Mathematical Theory of Cortical Micro-circuits" [Dileep George & Jeff Hawkins, PLoS Computational Biology, October 2009, Volume 5, Issue 10]. There were some bits of it that I had to treat as black boxes, but on the whole I found it comprehensible.
The core concern of the paper is to map a particular attempt to use computers to implement the Memory-Prediction framework of human intelligence to what is known about how nerve cells actually function in the cortex of the human brain. The specific machine methodology is called Hierarchical Temporal Memory (HTM). The article begins by explaining how HTM operates, then proceeds to map HTM processes to the cortex.
HTM structures are called nodes, but it should be noted that the nodes have extensive internal structure. They can have multiple inputs and outputs. They can have multiple "coincidence pattern matrices" and Markov chain processes. There are four major equations sets necessary for calibrating the nodes. I suggest you take a look at the HTM Technology Overview if you have not already. In particular, the authors assume the readers understand how Markov chains work, which is not obvious in this context.
It should be noted that HTM nodes are typically found in a hierarchy of nodes, and that information can move both up and down the hierarchy. The bottom of the hierarchy would typically correspond to sensory input, the top of the hierarchy to conceptual modes.
In fact, I found it easier to understand how the HTM worked internally when the authors started explaining the details in terms of neuron processes. The Markov chain likelihood circuit (Figure 4), in addition to mapping neurons to an aspect of an HTM node, makes it clearer that a Markov chain, in this context, is a set of information that has (or could have) predictive value. Markov chains are learned expectations about probabilities that events will occur in a time sequence.
This is a good example of a premise of the Memory-Prediction framework. The Markov chains are a sort of memory, yet they also are used to process information to make predictions. In computer science we tend to separate out memory from logical operations, but in the brain they are mostly inseparable.
As to the nervous system side of the mirror, I was not surprised to see a lot of the more complex work being performed by pyramidal cells. This neuron type appears to be quite differentiated from the more ordinary neurons that mainly relay information between muscles or sensory cells and the brain. Their very size and location in the cortex (particularly in layers 2, 3, and 5) should arose anyone's curiosity. Whether they really play the roles assigned to them here is not generally known, but hypotheses are made that should be testable.
The paper also covers the use of HTMs to recognize visual objects. Since much of the work done by Numenta and others using HTMs is in this field, I won't comment further here except to say that I found the work on the subjective contour effect particularly intriguing (example of subjective contours: Kanizsa triangle).
Merely categorizing visual objects is a more difficult problem that was originally thought by computer scientists working on Artificial Intelligence (AI). It is not learning about the successes with HTMs with pattern recognition that excites me. It is the way that it is done, and the promise that implies. I want to understand how the brain works in detail, but the ultimate goal is to understand intelligence, awareness, and understanding itself. The way HTMs process information, including the flowing of information both up and down the hierarchy, seems like a necessary condition for attacking these problems of higher intelligence. I don't think anyone thinks HTMs will prove to be entirely sufficient, but they seem like a good starting place for further physical and philosophical investigations.
The core concern of the paper is to map a particular attempt to use computers to implement the Memory-Prediction framework of human intelligence to what is known about how nerve cells actually function in the cortex of the human brain. The specific machine methodology is called Hierarchical Temporal Memory (HTM). The article begins by explaining how HTM operates, then proceeds to map HTM processes to the cortex.
HTM structures are called nodes, but it should be noted that the nodes have extensive internal structure. They can have multiple inputs and outputs. They can have multiple "coincidence pattern matrices" and Markov chain processes. There are four major equations sets necessary for calibrating the nodes. I suggest you take a look at the HTM Technology Overview if you have not already. In particular, the authors assume the readers understand how Markov chains work, which is not obvious in this context.
It should be noted that HTM nodes are typically found in a hierarchy of nodes, and that information can move both up and down the hierarchy. The bottom of the hierarchy would typically correspond to sensory input, the top of the hierarchy to conceptual modes.
In fact, I found it easier to understand how the HTM worked internally when the authors started explaining the details in terms of neuron processes. The Markov chain likelihood circuit (Figure 4), in addition to mapping neurons to an aspect of an HTM node, makes it clearer that a Markov chain, in this context, is a set of information that has (or could have) predictive value. Markov chains are learned expectations about probabilities that events will occur in a time sequence.
This is a good example of a premise of the Memory-Prediction framework. The Markov chains are a sort of memory, yet they also are used to process information to make predictions. In computer science we tend to separate out memory from logical operations, but in the brain they are mostly inseparable.
As to the nervous system side of the mirror, I was not surprised to see a lot of the more complex work being performed by pyramidal cells. This neuron type appears to be quite differentiated from the more ordinary neurons that mainly relay information between muscles or sensory cells and the brain. Their very size and location in the cortex (particularly in layers 2, 3, and 5) should arose anyone's curiosity. Whether they really play the roles assigned to them here is not generally known, but hypotheses are made that should be testable.
The paper also covers the use of HTMs to recognize visual objects. Since much of the work done by Numenta and others using HTMs is in this field, I won't comment further here except to say that I found the work on the subjective contour effect particularly intriguing (example of subjective contours: Kanizsa triangle).
Merely categorizing visual objects is a more difficult problem that was originally thought by computer scientists working on Artificial Intelligence (AI). It is not learning about the successes with HTMs with pattern recognition that excites me. It is the way that it is done, and the promise that implies. I want to understand how the brain works in detail, but the ultimate goal is to understand intelligence, awareness, and understanding itself. The way HTMs process information, including the flowing of information both up and down the hierarchy, seems like a necessary condition for attacking these problems of higher intelligence. I don't think anyone thinks HTMs will prove to be entirely sufficient, but they seem like a good starting place for further physical and philosophical investigations.
Friday, October 23, 2009
On Bayesian Belief Propagation
Towards a Mathematical Understanding of Cortical Micro-circuits [Dileep George & Jeff Hawkins, PLoS Computational Biology, October 2009, Volume 5, Issue 10] assumes some knowledge of Bayesian Belief Propagation. I was hoping the article would explain this topic as it went along, but apparently, to AI specialists, this is a well-known area. I found the Wikipedia entry, belief propagation, jumps into mathematical formulism rather quickly. Some words of explanation without math symbols would probably help many people who are interested in machine understanding; that is my goal here. If some of you Bayesian belief propagation experts think I have it wrong, or want to add anything, feel free to add comments. I have ordered a copy of the classic work on the subject, Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference , and so hope to be more fluent in this area at a later date.
, and so hope to be more fluent in this area at a later date.
Bayesian Belief Propagation (BBP) was formulated by Judea Pearl, who later authored Probabilistic Reasoning in Intelligent Systems. It appears to be a system for determining unknown probabilities within certain types of complex systems. Let's start with a review of a very simple probability model.
Much of early probability work was formulated in terms of a pair of ordinary gambling dice, six-sided cubes with faces numbered one through six. Thrown many times, they make a nice distribution pattern of numbers two through twelve. It can be shown with a little math and logic that there are percentages that are expected for each of these numbers. If you make a large number of dice throws, say more than 100, and you get results that differ by very much from the expected distribution of results, you may be looking at one of two things. It is possible that you have a distribution skewed purely by chance. On the other hand, you might want to investigate whether your dice and throwing systems are physically constructed to be truly random in the results they give.
Now imagine a black box, say the size of a shoe box. If you shake the box and then stop shaking, it gives you a number. In fact, imagine a room with a variety of such boxes. You shake them, keeping tracks of the resulting numbers for each. If one box consistently gives numbers between 2 and 12 inclusive, and the frequencies for each number match the pattern that we believe two dice would give, then we can conclude that the internal mechanism of the box, whatever it is, has a probability distribution that is created by the same logic that creates the dice probability distribution. There might even be a tiny pair of nano-dice inside.
In computer programming we tend to think in purely causal mechanics. If something does not happen as expected, we have a bug in our program. But in the case of living groups of biological neurons we cannot (so far) look at the inner mechanics of each neuron while watching how the whole group operates. However, if we can control the inputs and read the outputs of a system, then, if we can do the math, we might figure out the probabilities of individual neurons firing given known inputs from the other neurons in the system.
Formally, BBP allows us to calculate the probability characteristics for nodes we can't observe directly, if we can observe enough of the rest of the system. A node does not need to be a neuron. In an AI system, a node is a processing unit with inputs, outputs, or both, that connect it to the system of nodes in question. In our case the nodes are part of a Bayesian network, also known as a belief network. Communication (or messaging) within the network is in terms of probabilities. (See also Bayesian probability)
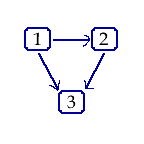
Think of a network of three people, where each of the people represents a node. Let there be a piece of paper we will call the message (it is blank; the paper is the message, in this case). Let each person have a single die and the rule: if you have the message, throw the die. If it comes up a one, a two, or a three, pass the message to the left. Otherwise, pass it to the right. If we watch the game progress, the message moves around or back and forth in a random pattern. However, it is not a Bayesian network, because it is cyclical. Bayesian networks are not cyclic. Messages more only in one direction.
Now start a series of games in which the message is always handed to person 1 (node 1). Person 1 throws the die and passes the message to person 2 if the result is 3 or less, and to person 3 if the result is 3 or more. Person 2 also throws a die and simply holds the message if the result is 3 or less, but passes if to person 3 if the result is 3 or more. When person 3 gets a message the game is over.
It is a simple game and a tad boring, but if we focus on the propagation time, the number of die throws from the beginning of a game until the end of a game, we can see a set of variations. Over the long run they should form a probability distribution of the times.
Now change the rules slightly. Say person 2 forwards the message if the die comes out 2 or higher. The range of possible results does not change, but the probability distribution will.
Now suppose you know about this type of game, but you can't see the game because it is in a tent. You see a message handed in, and can time how long it is before the message is handed back out by person 3.
By keeping track of the times, you can get the probability distribution. That should tell you the exact rules of the game being played, including the probability that person 1 will give the message directly to person 3, and how long person 2 might keep the message before passing it.
In more complex networks, you need to pin down the probabilities at more of the nodes, if you want to be able to characterize the probability rules for an unknown node.
Which is what the BBP algorithm is supposed to do. It calculates the probabilities for an unobservable node based on the observed nodes.
Bayesian Belief Propagation (BBP) was formulated by Judea Pearl, who later authored Probabilistic Reasoning in Intelligent Systems. It appears to be a system for determining unknown probabilities within certain types of complex systems. Let's start with a review of a very simple probability model.
Much of early probability work was formulated in terms of a pair of ordinary gambling dice, six-sided cubes with faces numbered one through six. Thrown many times, they make a nice distribution pattern of numbers two through twelve. It can be shown with a little math and logic that there are percentages that are expected for each of these numbers. If you make a large number of dice throws, say more than 100, and you get results that differ by very much from the expected distribution of results, you may be looking at one of two things. It is possible that you have a distribution skewed purely by chance. On the other hand, you might want to investigate whether your dice and throwing systems are physically constructed to be truly random in the results they give.
Now imagine a black box, say the size of a shoe box. If you shake the box and then stop shaking, it gives you a number. In fact, imagine a room with a variety of such boxes. You shake them, keeping tracks of the resulting numbers for each. If one box consistently gives numbers between 2 and 12 inclusive, and the frequencies for each number match the pattern that we believe two dice would give, then we can conclude that the internal mechanism of the box, whatever it is, has a probability distribution that is created by the same logic that creates the dice probability distribution. There might even be a tiny pair of nano-dice inside.
In computer programming we tend to think in purely causal mechanics. If something does not happen as expected, we have a bug in our program. But in the case of living groups of biological neurons we cannot (so far) look at the inner mechanics of each neuron while watching how the whole group operates. However, if we can control the inputs and read the outputs of a system, then, if we can do the math, we might figure out the probabilities of individual neurons firing given known inputs from the other neurons in the system.
Formally, BBP allows us to calculate the probability characteristics for nodes we can't observe directly, if we can observe enough of the rest of the system. A node does not need to be a neuron. In an AI system, a node is a processing unit with inputs, outputs, or both, that connect it to the system of nodes in question. In our case the nodes are part of a Bayesian network, also known as a belief network. Communication (or messaging) within the network is in terms of probabilities. (See also Bayesian probability)
Think of a network of three people, where each of the people represents a node. Let there be a piece of paper we will call the message (it is blank; the paper is the message, in this case). Let each person have a single die and the rule: if you have the message, throw the die. If it comes up a one, a two, or a three, pass the message to the left. Otherwise, pass it to the right. If we watch the game progress, the message moves around or back and forth in a random pattern. However, it is not a Bayesian network, because it is cyclical. Bayesian networks are not cyclic. Messages more only in one direction.
Now start a series of games in which the message is always handed to person 1 (node 1). Person 1 throws the die and passes the message to person 2 if the result is 3 or less, and to person 3 if the result is 3 or more. Person 2 also throws a die and simply holds the message if the result is 3 or less, but passes if to person 3 if the result is 3 or more. When person 3 gets a message the game is over.
It is a simple game and a tad boring, but if we focus on the propagation time, the number of die throws from the beginning of a game until the end of a game, we can see a set of variations. Over the long run they should form a probability distribution of the times.
Now change the rules slightly. Say person 2 forwards the message if the die comes out 2 or higher. The range of possible results does not change, but the probability distribution will.
Now suppose you know about this type of game, but you can't see the game because it is in a tent. You see a message handed in, and can time how long it is before the message is handed back out by person 3.
By keeping track of the times, you can get the probability distribution. That should tell you the exact rules of the game being played, including the probability that person 1 will give the message directly to person 3, and how long person 2 might keep the message before passing it.
In more complex networks, you need to pin down the probabilities at more of the nodes, if you want to be able to characterize the probability rules for an unknown node.
Which is what the BBP algorithm is supposed to do. It calculates the probabilities for an unobservable node based on the observed nodes.
Saturday, October 17, 2009
Bottom Up Machine Understanding
The first paragraph of "Towards a Mathematical Theory of Cortical Micro-circuits" [Dileep George & Jeff Hawkins, PLoS Computational Biology, October 2009, Volume 5, Issue 10] states:
Understanding the computational and informtion processing roles of cortical circuitry is one of the oustanding problems in neuroscience. ... the data are not sufficient to derive a computational theory in a purely bottom-up fashion
My own cortex, probably not wanting to give itself a headache by proceeding too rapidly into what looks like a dense and difficult paper, immediately drifted off into thoughts on deriving a computational theory in a purely bottom-up fashion.
The closer we get to the physical bottom, the easier it seems to be to understand that the project might work. Suppose we could model an entire human brain at the molecular level. We imagine a scanner that can tell us, for a living person who we admit is intelligent and conscious, where each molecule is to a sufficient degree of exactitude. We also would have a computational system for the rules of molecular physics, and appropriate inputs and outputs.
Unless you believe that the human mind is not material (a dualist or idealist philosophic view), such a molecular-detail model should run like a human brain. At first it should think (and talk and act, to the extent the outputs allow) exactly like the person whose brain was scanned.
However, that does not mean scientists would understand how the brain works, or how a computational machine could exhibit understanding. Reproducing a phenomena and understanding a phenomena are not the same thing. The advantage of such a molecular computional brain model would be that we could run experiments on it in a way that could not be done on human beings or even on other mammals. We could start inputting and tracing data flows. We could interrupt and view the model in detail at any time. We could change parameters and isolate subsystems. Perhaps, further in the future, such a model could even be constructed without having to scan a human brain for the initial state.
At present, for a bottoms-up approach that might actually be workable in less than a decade, we would probably want to do a neuron-by-neuron model (probably with all the non-neural supporting cells in the brain as well). However, a lot of new issues arise even at this seemingly low level, even if we presume we have some way to scan into the model all of the often-complicated axon to dendrite paths and synapses. If learning is indeed based on synapse strength (Hebbian hypothesis), we would need both a good model for synapse dynamics and a detailed original state of synapses. This would require modeling the synapses themselves at the molecular level, or perhaps one-level up at the some molecular aggregate level. In effect it would not be possible to model an adult brain that has exhibited intelligence and understanding. We would need to start with a baby brain and hope that it would go through a pattern of neural information development similar to that of a human child.
A complete neural-level model would be much easier to test intelligence hypothesese on than a molecular-level model. It would not in itelf indicate that we understand how humans understand the world. By running the model in two parallel instances (with identical starting states), but with selected malfunctions, we could probably isolate most of the sub-systems required for intelligence. This should help us build a comprehensible picture of how intelligence operates once it is established and of how it can be constructed by neural circuits from whatever the raw ingredients of intelligence turn out to be.
Despite our lack of such complete bottom-up models, I don't think it is too early to try to reconstruct how the brain works, or how to make machines intelligent. The paper outlines the HTM approach to this subject. HTM was based on a great deal of prior work in neuroscience and in modeling neural aggregates with computers. Often in science success has come from the combination of bottom-up and top-down approaches. Biological species, and fossil species, were long catalogued and studied before Darwin's theory of evolution revealed the connections between species. Darwin did not invent the concept of evolution of species, or of inherited traits, which many scientists already believed were shown by the fossil record and living organisms. He added the concept of natural selection, and suddenly evolution made sense. The whole picture popped into view in a way that any intelligent human being could see.
Understanding the computational and informtion processing roles of cortical circuitry is one of the oustanding problems in neuroscience. ... the data are not sufficient to derive a computational theory in a purely bottom-up fashion
My own cortex, probably not wanting to give itself a headache by proceeding too rapidly into what looks like a dense and difficult paper, immediately drifted off into thoughts on deriving a computational theory in a purely bottom-up fashion.
The closer we get to the physical bottom, the easier it seems to be to understand that the project might work. Suppose we could model an entire human brain at the molecular level. We imagine a scanner that can tell us, for a living person who we admit is intelligent and conscious, where each molecule is to a sufficient degree of exactitude. We also would have a computational system for the rules of molecular physics, and appropriate inputs and outputs.
Unless you believe that the human mind is not material (a dualist or idealist philosophic view), such a molecular-detail model should run like a human brain. At first it should think (and talk and act, to the extent the outputs allow) exactly like the person whose brain was scanned.
However, that does not mean scientists would understand how the brain works, or how a computational machine could exhibit understanding. Reproducing a phenomena and understanding a phenomena are not the same thing. The advantage of such a molecular computional brain model would be that we could run experiments on it in a way that could not be done on human beings or even on other mammals. We could start inputting and tracing data flows. We could interrupt and view the model in detail at any time. We could change parameters and isolate subsystems. Perhaps, further in the future, such a model could even be constructed without having to scan a human brain for the initial state.
At present, for a bottoms-up approach that might actually be workable in less than a decade, we would probably want to do a neuron-by-neuron model (probably with all the non-neural supporting cells in the brain as well). However, a lot of new issues arise even at this seemingly low level, even if we presume we have some way to scan into the model all of the often-complicated axon to dendrite paths and synapses. If learning is indeed based on synapse strength (Hebbian hypothesis), we would need both a good model for synapse dynamics and a detailed original state of synapses. This would require modeling the synapses themselves at the molecular level, or perhaps one-level up at the some molecular aggregate level. In effect it would not be possible to model an adult brain that has exhibited intelligence and understanding. We would need to start with a baby brain and hope that it would go through a pattern of neural information development similar to that of a human child.
A complete neural-level model would be much easier to test intelligence hypothesese on than a molecular-level model. It would not in itelf indicate that we understand how humans understand the world. By running the model in two parallel instances (with identical starting states), but with selected malfunctions, we could probably isolate most of the sub-systems required for intelligence. This should help us build a comprehensible picture of how intelligence operates once it is established and of how it can be constructed by neural circuits from whatever the raw ingredients of intelligence turn out to be.
Despite our lack of such complete bottom-up models, I don't think it is too early to try to reconstruct how the brain works, or how to make machines intelligent. The paper outlines the HTM approach to this subject. HTM was based on a great deal of prior work in neuroscience and in modeling neural aggregates with computers. Often in science success has come from the combination of bottom-up and top-down approaches. Biological species, and fossil species, were long catalogued and studied before Darwin's theory of evolution revealed the connections between species. Darwin did not invent the concept of evolution of species, or of inherited traits, which many scientists already believed were shown by the fossil record and living organisms. He added the concept of natural selection, and suddenly evolution made sense. The whole picture popped into view in a way that any intelligent human being could see.
Labels:
dendrites,
Dileep George,
evolution,
HTMs,
intelligence,
Jeff Hawkins,
machine understanding,
models,
neurons,
synapses
Wednesday, October 14, 2009
Markov Chains for Brain Models
I got an email from Numenta today, telling me that Dileep George and Jeff Hawkins had a paper, "Towards a Mathematical Theory of Cortical Micro-circuits", published in the PLoS Computational Biology journal. Part of the abstract states:
“we describe how Bayesian belief propagation in a spatio-temporal hierarchical model, called
Hierarchical Temporal Memory (HTM), can lead to a mathematical model for cortical circuits. An HTM node is abstracted using a coincidence detector and a mixture of Markov chains.”
HTM is the model being used by Numenta and others to crack to machine understanding problem by making an abstract, computable model of the human cortex (brain). I figured the article would explain “Bayesian belief propagation” which parses into three words I understand. I knew I had run into the term “Markov chains” before, in probability theory and elsewhere. I thought I would just refresh my memory about good old Andrey Markov with Wikipedia. But the Markov chains article at Wikipedia was tough going, jumping into the math without clearly explaining it in English. The definition there was comprehensible: “a random process where all information about the future is contained in the present state.” That implies there is a set of rules, expressed as probabilities, so that if you know the current state of a system you can predict its future state probabilities. It neatly combines determinism with indeterminism. For a first impression, I found the Examples of Markov Chains article more helpful.
I thought I might find a better explanation on my book shelf. There was nothing in my Schaum’s Statistics, but my next guess (thank you, cortex) Schaum's Outline of Operations Research
by Richard Bronson and Govindasami Naadimuthu, has an entire chapter, “Finite Markov Chains,” starting on page 369.
Markov chains are a subset of Markov processes. Markov processes consist of a set of objects with a set of states for the objects. At each point in time each object must be in one of the states. As time progresses, “the probability that an object moves from one state to another state in one time period depends only on the two states,” the current state and the probabilities for the future states given the current state.
For example, in the board game Monopoly each “square” or piece of real estate is part of the set of objects. The two dice create a probability structure, the standard one for two dice. The probability that, at any point, a player will transition to the same point, the forward adjacent point, or any point beyond the 12th point forward is zero, because the dice can only roll numbers between 2 and 12. However, more typically there would be a set of states and a probability for the transition to each of the states, including the transition of remaining in the current state.
If there are N possible states, and you know all the probabilities for transitions, you can show this and manipulate it mathematically with a matrix P, the stochastic or transition matrix. There would be N rows and columns in P. As in all probability theory, in any row the probabilities add up to 1.
N=2 is the simplest meaningful number of states. Let’s call them black and white. It is really only interesting if the transitions are different. Say 90% of the time black transitions to white, but only 20% of the time white transitions to black. Then the matrix P would be
.1 .9
.8 .2
There is some ability to predict the future in a statistical way if you have a Markov chain like this. Without doing any math, you would expect over time that if you have only one object, it would probably be white. If it is black, probably the next state of the sequence flips to white, but if it is white, probably the next state will be white. If you have a large number of objects, you can know the likelihood that a given percentage of them will be white or black. Yet you can’t know for sure. Even the least likely state, all objects black, can occur at any time if each black stays black but each white transitions to black.
You can see that Markov chains might be used to represent the states of neurons or of collections of neurons. In my simple examples above, each object influences only its own future state. But in real systems often future state probabilities are determined by the states of a collection of objects. It could be a collection of transistors, or a collection of nerve cells, or HTM nodes.
“we describe how Bayesian belief propagation in a spatio-temporal hierarchical model, called
Hierarchical Temporal Memory (HTM), can lead to a mathematical model for cortical circuits. An HTM node is abstracted using a coincidence detector and a mixture of Markov chains.”
HTM is the model being used by Numenta and others to crack to machine understanding problem by making an abstract, computable model of the human cortex (brain). I figured the article would explain “Bayesian belief propagation” which parses into three words I understand. I knew I had run into the term “Markov chains” before, in probability theory and elsewhere. I thought I would just refresh my memory about good old Andrey Markov with Wikipedia. But the Markov chains article at Wikipedia was tough going, jumping into the math without clearly explaining it in English. The definition there was comprehensible: “a random process where all information about the future is contained in the present state.” That implies there is a set of rules, expressed as probabilities, so that if you know the current state of a system you can predict its future state probabilities. It neatly combines determinism with indeterminism. For a first impression, I found the Examples of Markov Chains article more helpful.
I thought I might find a better explanation on my book shelf. There was nothing in my Schaum’s Statistics, but my next guess (thank you, cortex) Schaum's Outline of Operations Research
by Richard Bronson and Govindasami Naadimuthu, has an entire chapter, “Finite Markov Chains,” starting on page 369.
Markov chains are a subset of Markov processes. Markov processes consist of a set of objects with a set of states for the objects. At each point in time each object must be in one of the states. As time progresses, “the probability that an object moves from one state to another state in one time period depends only on the two states,” the current state and the probabilities for the future states given the current state.
For example, in the board game Monopoly each “square” or piece of real estate is part of the set of objects. The two dice create a probability structure, the standard one for two dice. The probability that, at any point, a player will transition to the same point, the forward adjacent point, or any point beyond the 12th point forward is zero, because the dice can only roll numbers between 2 and 12. However, more typically there would be a set of states and a probability for the transition to each of the states, including the transition of remaining in the current state.
If there are N possible states, and you know all the probabilities for transitions, you can show this and manipulate it mathematically with a matrix P, the stochastic or transition matrix. There would be N rows and columns in P. As in all probability theory, in any row the probabilities add up to 1.
N=2 is the simplest meaningful number of states. Let’s call them black and white. It is really only interesting if the transitions are different. Say 90% of the time black transitions to white, but only 20% of the time white transitions to black. Then the matrix P would be
.1 .9
.8 .2
There is some ability to predict the future in a statistical way if you have a Markov chain like this. Without doing any math, you would expect over time that if you have only one object, it would probably be white. If it is black, probably the next state of the sequence flips to white, but if it is white, probably the next state will be white. If you have a large number of objects, you can know the likelihood that a given percentage of them will be white or black. Yet you can’t know for sure. Even the least likely state, all objects black, can occur at any time if each black stays black but each white transitions to black.
You can see that Markov chains might be used to represent the states of neurons or of collections of neurons. In my simple examples above, each object influences only its own future state. But in real systems often future state probabilities are determined by the states of a collection of objects. It could be a collection of transistors, or a collection of nerve cells, or HTM nodes.
Tuesday, October 6, 2009
Synaptic Transmission Puzzle
"Over the past twenty years, a wide variety of modes of synaptic transmission have been discovered, in addition to simple, chemically mediated increases in permeability leading to excitation and inhibiation. Such modes of transmission include electrical exictation and inhibition, combined chemical-electrical synapses, chemical synapted changes produced by reductions in memberane permeability, and prolonged synaptic potentials mediated by chemical reactions in the postsynaptic cell."
-- page 208, From Neuron to Brain, Second Edition, by Stephen W. Kuffler, John G. Nicholls, and A. Robert Martin; 1984, Sinauer Associates, Inc., Suderland, Massachusetts
In Jeff Hawkins' On Intelligence, he presents a predictive-memory model for human intelligence which he believes can serve as a basis for intelligent machines [which I call machine understanding to emphasize that the machines would not merely be mimicking surface features of human intelligence, as is the case with, for example, expert systems]. I agree with him that while neuroscience and computing science have made great progress in understanding many details of the human brain, and in writing software, we need to have an overview that allows us to make progress on the centrals issues that interest us. Thus, in Hawkins' model, he does not worry about the exact nature of neural synapses.
But at the very least, we should be aware of how complicated human synapses are. This should allow us a greater freedom of thought when modeling the mechanics of machine understanding than if we simply assumed synapses all work alike. I suspect the Hebbian learning model for neurons would benefit from considering that the real world may complex, and in that complexity there may be keys to progress that we leave out with overly simple models.
What struck me most about the above paragraph about synapses, however, is the role played by evolution. Charles Darwin wrote about the process of species creation, but we have long grown used to the idea that evolution takes place on a molecular level. Each nerve cell, presumably, contains the full set of genes of the organism, but many different types of synapses are manifested. There must be controlling, blueprint genes that tell the cells which typese of synapses they are to form as they develop. In turn, we can expect that many different blueprints have been tried over the last four million years or so. The most successful gave their human organisms survival advantages.
It would be interesting to know how much synaptic variation exists in the current human population. Is this variation responsible, or partly responsible, for variations in basic intelligence capabilities of human beings?
This brings us back to the hard-wiring versus plastic debate. Human beings are very adaptable, as is shown by their ability to learn any of thousands of human languages as a child. We tend to think that we are very plastic and programmable creatures. But nerve transmission speeds and synaptic types are hard wired, as is the basic design of the brain. One might say we have the hard-wired capability to be flexible.
And that is what we aim to build into the new machines: hard wiring (a stable system with a design we understand and can reproduce) that is capable of showing the flexibility required to exhibit intelligence and understanding.
-- page 208, From Neuron to Brain, Second Edition, by Stephen W. Kuffler, John G. Nicholls, and A. Robert Martin; 1984, Sinauer Associates, Inc., Suderland, Massachusetts
In Jeff Hawkins' On Intelligence, he presents a predictive-memory model for human intelligence which he believes can serve as a basis for intelligent machines [which I call machine understanding to emphasize that the machines would not merely be mimicking surface features of human intelligence, as is the case with, for example, expert systems]. I agree with him that while neuroscience and computing science have made great progress in understanding many details of the human brain, and in writing software, we need to have an overview that allows us to make progress on the centrals issues that interest us. Thus, in Hawkins' model, he does not worry about the exact nature of neural synapses.
But at the very least, we should be aware of how complicated human synapses are. This should allow us a greater freedom of thought when modeling the mechanics of machine understanding than if we simply assumed synapses all work alike. I suspect the Hebbian learning model for neurons would benefit from considering that the real world may complex, and in that complexity there may be keys to progress that we leave out with overly simple models.
What struck me most about the above paragraph about synapses, however, is the role played by evolution. Charles Darwin wrote about the process of species creation, but we have long grown used to the idea that evolution takes place on a molecular level. Each nerve cell, presumably, contains the full set of genes of the organism, but many different types of synapses are manifested. There must be controlling, blueprint genes that tell the cells which typese of synapses they are to form as they develop. In turn, we can expect that many different blueprints have been tried over the last four million years or so. The most successful gave their human organisms survival advantages.
It would be interesting to know how much synaptic variation exists in the current human population. Is this variation responsible, or partly responsible, for variations in basic intelligence capabilities of human beings?
This brings us back to the hard-wiring versus plastic debate. Human beings are very adaptable, as is shown by their ability to learn any of thousands of human languages as a child. We tend to think that we are very plastic and programmable creatures. But nerve transmission speeds and synaptic types are hard wired, as is the basic design of the brain. One might say we have the hard-wired capability to be flexible.
And that is what we aim to build into the new machines: hard wiring (a stable system with a design we understand and can reproduce) that is capable of showing the flexibility required to exhibit intelligence and understanding.
Saturday, October 3, 2009
The Amazing Genetics of Nerves
I'll start with a quote from Stephen W. Kuffler, John G. Nicholls and A. Robert Martin's From Neuron to Brain (second edition, page 177; 1984 Sinauer Associates Inc.):
"... conduction velocity plays a significant role in the scheme of organization of the nervous system. It varies by a factor of more than 100 in nerve fibers that transmit different information content. In general, nerves that conduct most rapidly (more than 100 m/sec) are involved in mediating rapid reflexes, such as those used for regulating posture. Slower conduction velocities are associated with less urgent tasks such as regulating the distribution of blood flow to various parts of the body, controlling the secrection of glands, or regulating the tone of visceral organs."
Presumably much of this fine-tuning was achieved in mammals long before humans evolved. It is a great example of what can be achieved with evolution through natural selection. Apparently there is a cost to speedy nerve connections. There must be genes that can be turned on to produce extra structural elements (proteins, fats, etc) that speed up transmission velocity. There must be controlling genes that turn the structural genes on and off during nerve development, as appropriate.
Given these possibilities, there must be an overall genetic blueprint for nerve transmission velocity types. This blueprint would have been fine-tuned over time through the survival of the fittest. Having high cost, fast transmission where needed, and low-cost slower transmission where that will do, would give a slight evolutionary advantage.
The issue of transmission speed would be relatively simple comparted to creating a genetic blueprint for the orders-of-magnitude more complex human brain. Yet the construction process would be similar. A variety of brain cell types were already developed by mammals and primates. Probably (please comment if you know!) more cell types, including synapse types, evolved (from the usual mutation + selection process) for the human brain. The overall structure of the brain could be one blueprint, but it is an extremely complicated one. We know it involves axons and dendrites often both connecting to neighboring neurons and running long distances to connect to neurons after bypassing thousands, millions, or billions of closer neighbors.
This could only happen through evolution. Again, we have Charles Darwin to thank for setting us on the right path to understanding both nature and ourselves. As to machine understanding, the human brain is our best blueprint.
"... conduction velocity plays a significant role in the scheme of organization of the nervous system. It varies by a factor of more than 100 in nerve fibers that transmit different information content. In general, nerves that conduct most rapidly (more than 100 m/sec) are involved in mediating rapid reflexes, such as those used for regulating posture. Slower conduction velocities are associated with less urgent tasks such as regulating the distribution of blood flow to various parts of the body, controlling the secrection of glands, or regulating the tone of visceral organs."
Presumably much of this fine-tuning was achieved in mammals long before humans evolved. It is a great example of what can be achieved with evolution through natural selection. Apparently there is a cost to speedy nerve connections. There must be genes that can be turned on to produce extra structural elements (proteins, fats, etc) that speed up transmission velocity. There must be controlling genes that turn the structural genes on and off during nerve development, as appropriate.
Given these possibilities, there must be an overall genetic blueprint for nerve transmission velocity types. This blueprint would have been fine-tuned over time through the survival of the fittest. Having high cost, fast transmission where needed, and low-cost slower transmission where that will do, would give a slight evolutionary advantage.
The issue of transmission speed would be relatively simple comparted to creating a genetic blueprint for the orders-of-magnitude more complex human brain. Yet the construction process would be similar. A variety of brain cell types were already developed by mammals and primates. Probably (please comment if you know!) more cell types, including synapse types, evolved (from the usual mutation + selection process) for the human brain. The overall structure of the brain could be one blueprint, but it is an extremely complicated one. We know it involves axons and dendrites often both connecting to neighboring neurons and running long distances to connect to neurons after bypassing thousands, millions, or billions of closer neighbors.
This could only happen through evolution. Again, we have Charles Darwin to thank for setting us on the right path to understanding both nature and ourselves. As to machine understanding, the human brain is our best blueprint.
Labels:
axons,
brain,
Charles Darwin,
dendrites,
evolution,
genetics,
machine understanding,
natural selection,
nerves
Tuesday, September 15, 2009
How I Spent My Summer
Obviously I have not spent time on the blog lately. I had a busy time indexing a technology book, and when that was done was behind on many other things. I have also been doing a considerable amount of studying on issues of machine understanding, but delayed my project of going through On Intelligence by Jeff Hawkins and explicating it. I have read it twice now; I am not ready for a third read. I did look at the web sites associated with the Hawkin's model, and will report on them when I have a chance to study them in more detail.
I am reading, or wading through, Neuron to Brain by Stephen W. Kuffler et al. The chapter on the structure of the visual cortex was near the front, which made interesting compare and contrast reading with On Intelligence. But I did not make the effort to write up my thoughts, and that must now wait for a vacation from other duties.
I have become better at tensor analysis, which had the added benefit of making Einstein's "The Foundation of the General Theory of Relativity" readable. I don't think tensors are going to be good models for neural networks, but the concept of invariance is well-developed with tensors and it seems central to the topic of maching understanding. By thinking about the structure of neurons in the brain, and invariance, I hope to at least exercise my mind in the vicinity of the problem.
Today I am fascinated by the possible application of metrics, inner-product spaces, and invariant angles to the question of how human babies construct their mental world. I was struck by the important of coordinating tactile senses with vision and auditory sensation. The main apparatus for this is the human arm. Excluding the hand, the arm consists of two big angles, one at the shoulder, the other at the elbow. There are a lot of degrees of freedom therein. To grab objects requires a lot of coordination. The angles are going to vary with muscle tone, which is controlled by the motor areas of the brain. But the general space should be an inner-product space. Changes of coordinates, say if the coordinate system was directed from the eyes, would not change the angles, lengths, or positions of the hands.
It makes me think about how flexible the human mind can be, and then contrast with how rigid people's thoughts can be. Once we learn about Euclidean space we tend to think we are walking around in it, with the ground as a two-dimensional plane. The idea that a coordinate system could be anchored by an imaginary line perpendicular to a line connnected the eyes strikes us as peculiar. Yet we use that coordinate system constantly, perhaps more than any other.
I am reading, or wading through, Neuron to Brain by Stephen W. Kuffler et al. The chapter on the structure of the visual cortex was near the front, which made interesting compare and contrast reading with On Intelligence. But I did not make the effort to write up my thoughts, and that must now wait for a vacation from other duties.
I have become better at tensor analysis, which had the added benefit of making Einstein's "The Foundation of the General Theory of Relativity" readable. I don't think tensors are going to be good models for neural networks, but the concept of invariance is well-developed with tensors and it seems central to the topic of maching understanding. By thinking about the structure of neurons in the brain, and invariance, I hope to at least exercise my mind in the vicinity of the problem.
Today I am fascinated by the possible application of metrics, inner-product spaces, and invariant angles to the question of how human babies construct their mental world. I was struck by the important of coordinating tactile senses with vision and auditory sensation. The main apparatus for this is the human arm. Excluding the hand, the arm consists of two big angles, one at the shoulder, the other at the elbow. There are a lot of degrees of freedom therein. To grab objects requires a lot of coordination. The angles are going to vary with muscle tone, which is controlled by the motor areas of the brain. But the general space should be an inner-product space. Changes of coordinates, say if the coordinate system was directed from the eyes, would not change the angles, lengths, or positions of the hands.
It makes me think about how flexible the human mind can be, and then contrast with how rigid people's thoughts can be. Once we learn about Euclidean space we tend to think we are walking around in it, with the ground as a two-dimensional plane. The idea that a coordinate system could be anchored by an imaginary line perpendicular to a line connnected the eyes strikes us as peculiar. Yet we use that coordinate system constantly, perhaps more than any other.
Wednesday, July 8, 2009
Numenta
While I am getting up to speed (a slow process, given my other commitments), there is no reason for someone who is interested in this topic to zoom to the cutting edge. A good place for a jump start, after you have read On Intelligence, is the Numenta web site. You can also check out the OnIntelligence.org web site, which sponsors some forums on Hawkins's predictive memory model of intelligence and has some links to related materials. Today I'll just describe what is at the Numenta site.
If you have not read On Intelligence, in particular Chapter 6, "How the Cortex Works," you can still get a lot out of reading materials at the Numenta site. However, I would advise reading the book first, old fashioned as that may sound.
You might be ready to jump right into "Hierarchical Temporal Memory Concepts, Theory and Terminology" by Jeff Hawkins and Dileep George. You are going to want to read it at some point. It is focused on HTMs (Hierarchical Temporal Memory technology). This is an attempt to implement the model of the human brain cortex, but in data-processing rather than biological terms. It is also the main technology being developed at Numenta.
On the other hand you may want to look at the HTM Technology Overview first. It is short and sweet, and also has a link to Problems That Fit HTMs. Of course if the HTM actually is a good model for the human cortex, HTMs should do well at problems that people (and often other mammals) do well at, but that computers, even using AI (artificial intelligence) techniques are not good at.
If you are a hands-on person, you could skip the theory and start with one of the software development kits. One is Vision Software, the other is NuPIC which now includes Vision. However, the NuPIC web page has a link to technical resources that would be important if you get serious about working with HTMs.
I'll write more about Numenta, just as I'll be writing more commentary on machine understanding and intelligence in general. I will be approaching HTMs from a critical perspective: do they implement a predictive memory model; is this the best implementation; and is the model really central to biological intelligence and machine understanding.
If you have not read On Intelligence, in particular Chapter 6, "How the Cortex Works," you can still get a lot out of reading materials at the Numenta site. However, I would advise reading the book first, old fashioned as that may sound.
You might be ready to jump right into "Hierarchical Temporal Memory Concepts, Theory and Terminology" by Jeff Hawkins and Dileep George. You are going to want to read it at some point. It is focused on HTMs (Hierarchical Temporal Memory technology). This is an attempt to implement the model of the human brain cortex, but in data-processing rather than biological terms. It is also the main technology being developed at Numenta.
On the other hand you may want to look at the HTM Technology Overview first. It is short and sweet, and also has a link to Problems That Fit HTMs. Of course if the HTM actually is a good model for the human cortex, HTMs should do well at problems that people (and often other mammals) do well at, but that computers, even using AI (artificial intelligence) techniques are not good at.
If you are a hands-on person, you could skip the theory and start with one of the software development kits. One is Vision Software, the other is NuPIC which now includes Vision. However, the NuPIC web page has a link to technical resources that would be important if you get serious about working with HTMs.
I'll write more about Numenta, just as I'll be writing more commentary on machine understanding and intelligence in general. I will be approaching HTMs from a critical perspective: do they implement a predictive memory model; is this the best implementation; and is the model really central to biological intelligence and machine understanding.
Tuesday, June 23, 2009
Theories of the Brain
As a summary, what Jeff Hawkins says on page 2 of On Intelligence seems accurate to me and note this was published in 2004:
All of my experience led me to the same conclusion. It is not that some scientists, computer software engineers, and philosophers have not looked at the problems that On Intelligence addresses. In retrospect, however, most of them made the same fundamental mistake. Characterize it as trying to replicate behavior instead of creating intelligence that replicates human intelligence and therefore human behavior. And one reason most people made the same mistake was because there was no good model of the brain available from the neuroscientists.
I have on my bookshelf The Formal Mechanics of Mind by Stephen N. Thomas. The inside cover blurb says "The author's intention is to provide an analysis of the nature of the mind, and of our knowledge of it—an analysis that solves or avoids longstanding philosophical problems and that fits well with the results of psychological and neuropsychological investigations of mental phenomena." It is a good book. Published in 1978, it is one of the best I had read before On Intelligence.
On the other hand we have the computer programming AI people. They did some pretty good work, but it is a cautionary tale. Most AI worked with very simple models of objects. AI did best, or appeared to do best, when dealing with certain higher human mental functions, like formal logic. But the brain does not appear to operate with formal logic. Humans invented formal logic. It may (or may not) serve as a basis for a theory of mathematics, as Bertrand Russel, A. N. Whitehead, Ludwig Wittgenstein, and John von Neuman attempted to show.
We will, of course, be using mathematics to understand "real" intelligence. Yet there is almost no math in On Intelligence. Before we can develop a math, or apply an existing branch of mathematics, to this problem we have to understand both the true nature of the problem and how the brain implements the solution, both structurally and dynamically.
I also have on my bookshelf, among other books on neural networks, Parallel Distributed Processing by James L. McClelland et. al. I wrote some computer programs to implement some of the models presented in the book. That was back in the late 1980's. The intelligence problem, then, seemed to be solvable in a piecemeal manner. Difference types of neural networks could be combined and improved until something approaching intelligence emerged. But my own attempts at building an intelligence model went nowhere, and I got involved in trying to save some redwood forests. The forests were clearcut despite my efforts, and I'll take Hawkins' word for it when he said that the neural network model had not made substantial progress in the 1990's. Again, neural network software and hardware became very good at certain things, notably pattern recognition. But while intelligent systems (humans) can recognize patters, apparently pattern recognition is not in itself the basis of intelligence.
Next up: Real Intelligence versus AI
Yet we have no productive theories about what intelligence is or how the brain works as a whole. Most neurobiologists don't think much about overall theories of the brain because they're engrossed in doing experiments to collect more data about the brain's many subsystems. And although legions of computer programmers have tried to make computers intelligent, they have failed. I believe they will continue to fail as long as they keep ignoring the differences between computers and brains.Of course later Hawkins discusses in some detail both neuroscience and attempts at creating human-like machine behavior with what we will call the old AI, or Artificial Intelligence.
All of my experience led me to the same conclusion. It is not that some scientists, computer software engineers, and philosophers have not looked at the problems that On Intelligence addresses. In retrospect, however, most of them made the same fundamental mistake. Characterize it as trying to replicate behavior instead of creating intelligence that replicates human intelligence and therefore human behavior. And one reason most people made the same mistake was because there was no good model of the brain available from the neuroscientists.
I have on my bookshelf The Formal Mechanics of Mind by Stephen N. Thomas. The inside cover blurb says "The author's intention is to provide an analysis of the nature of the mind, and of our knowledge of it—an analysis that solves or avoids longstanding philosophical problems and that fits well with the results of psychological and neuropsychological investigations of mental phenomena." It is a good book. Published in 1978, it is one of the best I had read before On Intelligence.
On the other hand we have the computer programming AI people. They did some pretty good work, but it is a cautionary tale. Most AI worked with very simple models of objects. AI did best, or appeared to do best, when dealing with certain higher human mental functions, like formal logic. But the brain does not appear to operate with formal logic. Humans invented formal logic. It may (or may not) serve as a basis for a theory of mathematics, as Bertrand Russel, A. N. Whitehead, Ludwig Wittgenstein, and John von Neuman attempted to show.
We will, of course, be using mathematics to understand "real" intelligence. Yet there is almost no math in On Intelligence. Before we can develop a math, or apply an existing branch of mathematics, to this problem we have to understand both the true nature of the problem and how the brain implements the solution, both structurally and dynamically.
I also have on my bookshelf, among other books on neural networks, Parallel Distributed Processing by James L. McClelland et. al. I wrote some computer programs to implement some of the models presented in the book. That was back in the late 1980's. The intelligence problem, then, seemed to be solvable in a piecemeal manner. Difference types of neural networks could be combined and improved until something approaching intelligence emerged. But my own attempts at building an intelligence model went nowhere, and I got involved in trying to save some redwood forests. The forests were clearcut despite my efforts, and I'll take Hawkins' word for it when he said that the neural network model had not made substantial progress in the 1990's. Again, neural network software and hardware became very good at certain things, notably pattern recognition. But while intelligent systems (humans) can recognize patters, apparently pattern recognition is not in itself the basis of intelligence.
Next up: Real Intelligence versus AI
Labels:
ai,
intelligence,
Jeff Hawkins,
mathematics,
On Intelligence
Thursday, June 18, 2009
On Passions and Machine Understanding
Today I started reading On Intelligence by Jeff Hawkins for the third time. The first time I read the book I was impressed. The second time I read the book I believe I understood the more difficult parts. This time I am reading the book with two agendas: commenting on it in-depth, and developing my own ideas, complete with a mathematical framework, for machine understanding.
On page 1 of the prologue Jeff writes:
Hopefully my interest in literature and writing, history, gardening, politics, and art will bring something to this enterprise. If nothing else, I can chronicle the field's development. And I hope to range into any topic that could be helpful in the endeavor, not just neuroscience and computer technology.
On page 1 of the prologue Jeff writes:
I suffer from passion attention deficit disorder (PADD). I am of the same temporal generation as Jeff Hawkins, a child of the space, computer, and nuclear age. I cannot even remember when I first wondered how people can be intelligent and conscious. Such wonder was in the air of the science fictions novels I read as a child. But I have other passions as well. So I have engaged in a variety of pursuits over the decades, only once in a while returning to the contemplation of machine understanding and its related issues of biology, philosophy, and technology.But I have a second passion that predates my interest in computers, one I view as more important. I am crazy about brains. I want to understand how the brain works, not just from a philosophical perspective, not just in a general way, but in a detailed nuts and bolts engineering way.
Hopefully my interest in literature and writing, history, gardening, politics, and art will bring something to this enterprise. If nothing else, I can chronicle the field's development. And I hope to range into any topic that could be helpful in the endeavor, not just neuroscience and computer technology.
Wednesday, April 8, 2009
The Cortex, Dogs, and Changes of Coordinates
I finished my second read-though of On Intelligence by Jeff Hawkins several weeks ago. I got a lot out of this reading, and even was able to follow the details of Chapter 6 which eluded me the first time. Despite good intentions I neglected to write down my much-provoked thoughts until now. I have been spending most of that time indexing the new edition of Windows Internals by Mark Russinovich et. al., which is interesting in an entirely different way: one sees the products of human intelligence, but it is obvious that there is no danger of a Windows operating system of the current style becoming intelligent or conscious, ever.
by Mark Russinovich et. al., which is interesting in an entirely different way: one sees the products of human intelligence, but it is obvious that there is no danger of a Windows operating system of the current style becoming intelligent or conscious, ever.
In addition to following Jeff's suggestions about noticing how my own mind works, I have been thinking about these matters while watching my dog, Hugo. Let's say he represents mammals in general. He may not have the big old cortex that Jeff admires so much, but he seems to be constantly using his little one to make predictions. Hugo has to make a lot of decisions, and he often freezes in place while making them. Come when called? Maybe, maybe not. A treat in hand might just mean being captured and taken indoors, or left out of a car ride. To make such decisions, I believe, Hugo has to predict outcomes.
Like most dogs, Hugo likes to chase thrown toys. He has come to associate arm movements with probable outcomes. He knows if you are throwing in a particular direction, and begins his run in that direction without waiting for the toy to be released. He expects the toy to appear in front of him. If it does not, he looks back. Will I go ahead and throw the toy past him, or throw it in another direction.
Do this a few times, and he stops dashing as soon as my arm is moving. He waits to see if and where where I actually throw the toy.
I also believe Hugo has a construct of the world very similar to our human construct. He navigates the real world with an ease that can only come from having an internal map of the world. He understands the three-dimensional nature of the world, and in particular that obstacles like a tree or a house can have space behind them.
All this means is that if we want to build cortex like machine designs, we can do a lot without having to recreate a human brain. A car as smart as Hugo could go anywhere it wants on roads without smashing into other cars. This reminds me of science fiction stories where human brains are disembodied and plugged directly into space ships.
So maybe our first goal should be to create animal-brain equivalents and see what can be done with them.
I just happen to be reviewing the branch of mathematics that deals with changes of coordinates. I've always wanted to understand quantum physics and general relativity better, so I occasionally break open a math book, because at some point you must do the math to know what the smart guys are talking about. It is clear to me that human brains, and probably mammal brains too, are pretty good at changes of coordinates. The fact that we construct a mental map of the world and so easily map visual, audio, and tactile coordinates to it and back again is pretty remarkable.
I am again about to review how invariants are treated in tensor mathematics. Maybe that has nothing to do with the ability of the cortex to navigate the world, but it just might. Our brains certainly are good at creating invariant memories and comparing them to real world experiences.
Using the cortex to analyze the cortex: now that is a wonder.
In addition to following Jeff's suggestions about noticing how my own mind works, I have been thinking about these matters while watching my dog, Hugo. Let's say he represents mammals in general. He may not have the big old cortex that Jeff admires so much, but he seems to be constantly using his little one to make predictions. Hugo has to make a lot of decisions, and he often freezes in place while making them. Come when called? Maybe, maybe not. A treat in hand might just mean being captured and taken indoors, or left out of a car ride. To make such decisions, I believe, Hugo has to predict outcomes.
Like most dogs, Hugo likes to chase thrown toys. He has come to associate arm movements with probable outcomes. He knows if you are throwing in a particular direction, and begins his run in that direction without waiting for the toy to be released. He expects the toy to appear in front of him. If it does not, he looks back. Will I go ahead and throw the toy past him, or throw it in another direction.
Do this a few times, and he stops dashing as soon as my arm is moving. He waits to see if and where where I actually throw the toy.
I also believe Hugo has a construct of the world very similar to our human construct. He navigates the real world with an ease that can only come from having an internal map of the world. He understands the three-dimensional nature of the world, and in particular that obstacles like a tree or a house can have space behind them.
All this means is that if we want to build cortex like machine designs, we can do a lot without having to recreate a human brain. A car as smart as Hugo could go anywhere it wants on roads without smashing into other cars. This reminds me of science fiction stories where human brains are disembodied and plugged directly into space ships.
So maybe our first goal should be to create animal-brain equivalents and see what can be done with them.
I just happen to be reviewing the branch of mathematics that deals with changes of coordinates. I've always wanted to understand quantum physics and general relativity better, so I occasionally break open a math book, because at some point you must do the math to know what the smart guys are talking about. It is clear to me that human brains, and probably mammal brains too, are pretty good at changes of coordinates. The fact that we construct a mental map of the world and so easily map visual, audio, and tactile coordinates to it and back again is pretty remarkable.
I am again about to review how invariants are treated in tensor mathematics. Maybe that has nothing to do with the ability of the cortex to navigate the world, but it just might. Our brains certainly are good at creating invariant memories and comparing them to real world experiences.
Using the cortex to analyze the cortex: now that is a wonder.
Labels:
brain,
coordinates,
cortex,
Hugo,
intelligence,
invariants,
Jeff Hawkins,
maps,
On Intelligence,
prediction,
tensors
Wednesday, January 21, 2009
Gambling, Addiction and Prediction
Why do people love to gamble? True, there is a range of how much various people like to gamble. At one end there are people are (or pretend to be) bored by it (I exclude people who, for whatever reason, won’t even try games of chance or skill). At the other end are people who lose their savings, homes, and families, or even fingers and lives to legal and illegal gambling operations.
It may all have to do with the brain’s built-in prediction mechanisms.
According to Jeff Hawkins’s theory of the sequential and predictive basis of human intelligence, the primary intelligent function of the brain is to remember sequences of data and use that memory to predict future sequences of data. This is true both for sensory data that we think of as naturally sequential, like the notes in a music tune, and for sensory data that we normally think of as non-sequential, like the features in a human face. According to the theory we construct a model of a human face from sequences of visual input (supplemented by other data, like touching one’s own face). If we see an eye, we expect to see a sequence of other features: another eye, a nose, mouth, eyebrows, hair, chin, ears. We expect to hear a voice when a mouth moves, but not when an eye blinks.
An important element in building a model of the world is surprise. Using memory, the brain predicts what it expects to see, hear, and feel next. When something different occurs, the element of surprise turns on higher functions in the brain. We may look at something more closely. Perhaps it is a face, but it is a strange face. Is this a sign of danger? Friend or foe, we need to memorize the new face and whatever we associate with it (perhaps the face belongs to someone who is being introduced by a friend; we need to remember that association, or the physical place where we met the person).
There is a bit of a nervous rush when a prediction is made that turns out to be false. The mind gears up to determine why it made a false prediction, both in order to deal with the unexpected situation and to be able to predict it in the future. Probably this rush is partly neurochemical. We’ll call it a bit of adrenaline, although it is possibly based on another neurotransmitter or hormone. Adrenaline rush is the lay term I will use.
Games can teach, and they can while the time away. Even when they are not played for money or prizes, they can have an addictive quality. In almost every game an element of prediction is involved. The outcome provides relief if it was predicted, and a rush of neural activity if it was not predicted.
Generally, people like adrenaline rushes, especially in small doses. They like a thrill more than they like boredom. Games are played partly because they provide small, safe levels of thrill in situations that would otherwise being predictable and boring.
Gambling involves making a prediction. It involves two highs for the human brain. Most of us enjoy winning. Getting money from winning gives the same motivation as getting a snack, affection, or a pay check.
I believe that it is losing, however, that makes gambling addictive. When you lose in a random game of chance, your brain is fooled. It made a prediction. It was surprised by the outcome. Now it is designed to frantically memorize what happened and construct a way of making a correct prediction.
Gamblers often come to believe, after a string of losses, that they are about to make a correct prediction or a series of correct predictions. This is how your brain works: long experience has taught it that nature is a set of sequences, and past sequences can predict future sequences. The brain is fooled by the artificial construction of random events like dice throws, roulette wheel spins, and card deals. Worse, there is a sometimes-confusing element of predictability to some of this (two dice will roll a seven more often than a two; in poker three of a kind comes up more often than four of a kind) that tends to reinforce the brains belief that it can make sense out of randomness. The brain persists in the false belief that random events become predictable if only you keep placing bets long enough.
There is a rush when losing. People, on a chemical level, don’t feel pain when they lose. The chips or money they gamble is abstract, removed from the necessities or pleasures they could buy if had not lost. But the loss forces the higher intelligence centers of the brain to gear up. It is like taking a tiny bit of a stimulant. It is pleasurable.
This is often why otherwise highly intelligent individuals will lose vast sums of money in casinos. It is precisely like drug addiction. They may, at some conscious level, when away from a casino, coldly say that they understand they cannot beat a random game with odds set so that the house wins. But in the casino they cannot get out of the loop of feeding themselves tiny bits of adrenaline with each wager, win or lose.
It may all have to do with the brain’s built-in prediction mechanisms.
According to Jeff Hawkins’s theory of the sequential and predictive basis of human intelligence, the primary intelligent function of the brain is to remember sequences of data and use that memory to predict future sequences of data. This is true both for sensory data that we think of as naturally sequential, like the notes in a music tune, and for sensory data that we normally think of as non-sequential, like the features in a human face. According to the theory we construct a model of a human face from sequences of visual input (supplemented by other data, like touching one’s own face). If we see an eye, we expect to see a sequence of other features: another eye, a nose, mouth, eyebrows, hair, chin, ears. We expect to hear a voice when a mouth moves, but not when an eye blinks.
An important element in building a model of the world is surprise. Using memory, the brain predicts what it expects to see, hear, and feel next. When something different occurs, the element of surprise turns on higher functions in the brain. We may look at something more closely. Perhaps it is a face, but it is a strange face. Is this a sign of danger? Friend or foe, we need to memorize the new face and whatever we associate with it (perhaps the face belongs to someone who is being introduced by a friend; we need to remember that association, or the physical place where we met the person).
There is a bit of a nervous rush when a prediction is made that turns out to be false. The mind gears up to determine why it made a false prediction, both in order to deal with the unexpected situation and to be able to predict it in the future. Probably this rush is partly neurochemical. We’ll call it a bit of adrenaline, although it is possibly based on another neurotransmitter or hormone. Adrenaline rush is the lay term I will use.
Games can teach, and they can while the time away. Even when they are not played for money or prizes, they can have an addictive quality. In almost every game an element of prediction is involved. The outcome provides relief if it was predicted, and a rush of neural activity if it was not predicted.
Generally, people like adrenaline rushes, especially in small doses. They like a thrill more than they like boredom. Games are played partly because they provide small, safe levels of thrill in situations that would otherwise being predictable and boring.
Gambling involves making a prediction. It involves two highs for the human brain. Most of us enjoy winning. Getting money from winning gives the same motivation as getting a snack, affection, or a pay check.
I believe that it is losing, however, that makes gambling addictive. When you lose in a random game of chance, your brain is fooled. It made a prediction. It was surprised by the outcome. Now it is designed to frantically memorize what happened and construct a way of making a correct prediction.
Gamblers often come to believe, after a string of losses, that they are about to make a correct prediction or a series of correct predictions. This is how your brain works: long experience has taught it that nature is a set of sequences, and past sequences can predict future sequences. The brain is fooled by the artificial construction of random events like dice throws, roulette wheel spins, and card deals. Worse, there is a sometimes-confusing element of predictability to some of this (two dice will roll a seven more often than a two; in poker three of a kind comes up more often than four of a kind) that tends to reinforce the brains belief that it can make sense out of randomness. The brain persists in the false belief that random events become predictable if only you keep placing bets long enough.
There is a rush when losing. People, on a chemical level, don’t feel pain when they lose. The chips or money they gamble is abstract, removed from the necessities or pleasures they could buy if had not lost. But the loss forces the higher intelligence centers of the brain to gear up. It is like taking a tiny bit of a stimulant. It is pleasurable.
This is often why otherwise highly intelligent individuals will lose vast sums of money in casinos. It is precisely like drug addiction. They may, at some conscious level, when away from a casino, coldly say that they understand they cannot beat a random game with odds set so that the house wins. But in the casino they cannot get out of the loop of feeding themselves tiny bits of adrenaline with each wager, win or lose.
Labels:
addiction,
brain,
gambling,
intelligence,
memory,
prediction,
sequences,
surprise
Thursday, January 8, 2009
Welcome to Machine Understanding
I have been interested in the idea of intelligent, understanding, conscious machines (computers and robots) since I was a child. How could a fan of science fiction books and movies not be? At some point I started wondering how the human mind itself could be intelligent, understanding, and conscious. During my life I have periodically returned to that theme.
A relatively recent wake-up call for me was On Intelligence by Jeff Hawkins. I read the book last year and I am re-reading it now. So most of these early blog entries are inspired by statements from the book. I am more than half-way through the book, well into the nuts-and-bolts of Chapter 6, so I will probably both comment on what I am reading and go back to various passages in the front half of the book.
A few years ago my article Indexing Books: Lessons in Language Computations was published by the Key Words, the Bulletin of the American Society for Indexing. I don't want to discourage you from reading the article, but let me sum it up: if a machine can't read with comprehension, it can't create a high-quality index for a text. Most people think using a computer to generate a good index of a text should be an easy accomplishment.
I chose the term "machine understanding" over AI, artificial intelligence, because I agree with Jeff that the AI field has mainly been a failure. Perhaps I should have called it "human understanding," since we don't really have a good understanding of why humans can understand things, exhibit intelligence, and are conscious.
This blog is mainly for me to keep a record of my thoughts, but if anyone else stumbles across it I hope I can introduce them to the ideas of people who work in this fascinating field.
A relatively recent wake-up call for me was On Intelligence by Jeff Hawkins. I read the book last year and I am re-reading it now. So most of these early blog entries are inspired by statements from the book. I am more than half-way through the book, well into the nuts-and-bolts of Chapter 6, so I will probably both comment on what I am reading and go back to various passages in the front half of the book.
A few years ago my article Indexing Books: Lessons in Language Computations was published by the Key Words, the Bulletin of the American Society for Indexing. I don't want to discourage you from reading the article, but let me sum it up: if a machine can't read with comprehension, it can't create a high-quality index for a text. Most people think using a computer to generate a good index of a text should be an easy accomplishment.
I chose the term "machine understanding" over AI, artificial intelligence, because I agree with Jeff that the AI field has mainly been a failure. Perhaps I should have called it "human understanding," since we don't really have a good understanding of why humans can understand things, exhibit intelligence, and are conscious.
This blog is mainly for me to keep a record of my thoughts, but if anyone else stumbles across it I hope I can introduce them to the ideas of people who work in this fascinating field.
Subscribe to:
Comments (Atom)
